728x90
선택 정렬
- 정의 : 첫번째 자리에 가장 값은 값을 찾아 넣고 다음 Index 에 그 다음 작은 값을 찾아서 넣는다. 이 과정을 배열이 끝날 때까지 반복 하고 정렬된 배열을 출력 한다.
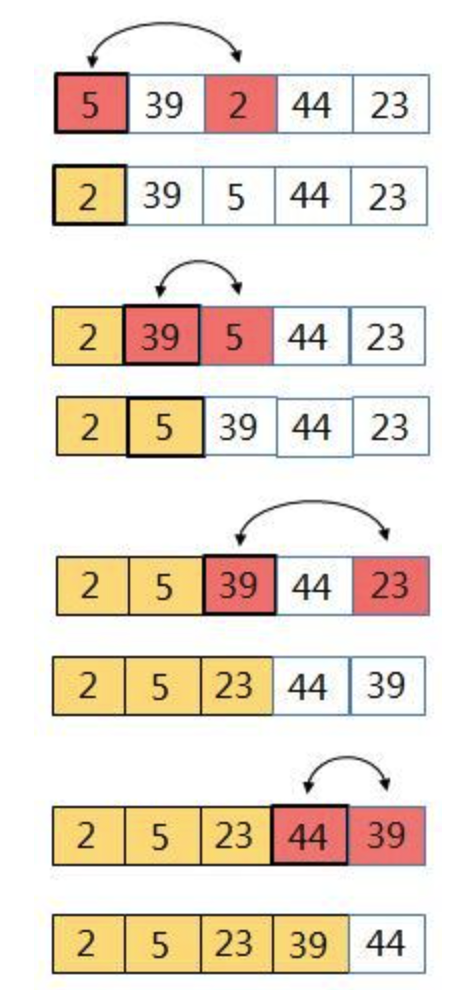
- 코드(KOTLIN) : 아래 코드에서 알 수 있을 듯 이중 for 루프를 이용해서 위의 그림의 동작을 수행한다. 시간 복잡도는 O(N^2) 를 가진다.
import java.io.*
import java.util.*
fun main(args: Array<String>) {
val br = BufferedReader(InputStreamReader(System.`in`))
val n = br.readLine().toInt()
val st = StringTokenizer(br.readLine())
var numbers = IntArray(n) {
st.nextToken().toInt()
}
// 선택 정렬
for (i in 0 until n - 1) {
var min = numbers[i]
for (j in (i + 1) until n) {
if (min > numbers[j]) {
// 현재 값보다 작은 값과 위치 변경
val temp = min
numbers[i] = numbers[j]
numbers[j] = temp
break
}
}
}
for (num in numbers) {
print("$num ")
}
}버블 정렬
- 정의 : 인접한 두 원소를 비교하여 정렬 한다.

- 코드(KOTLIN)
import java.io.*
import java.util.*
fun main(args: Array<String>) {
val br = BufferedReader(InputStreamReader(System.`in`))
val n = br.readLine().toInt()
val st = StringTokenizer(br.readLine())
val numbers = IntArray(n) {
st.nextToken().toInt()
}
// 버블 정렬
for (i in n downTo 1) {
for (j in 0 until (i - 1)) {
if (numbers[j] > numbers[j + 1]) {
val temp = numbers[j]
numbers[j] = numbers[j + 1]
numbers[j + 1] = temp
}
}
}
for (num in numbers) {
print("$num ")
}
}삽입 정렬
- 정의 : 삽입 정렬을 우선 배열의 한 원소인 key라는 값을 우선 가지고 있고, 이 key를 알맞은 자리에 삽입하면 됩니다. key보다 큰 값은 하나하니씩 밀어버리고 key보다 작은 값을 만났으때 그 뒷자리에 삽입한다.
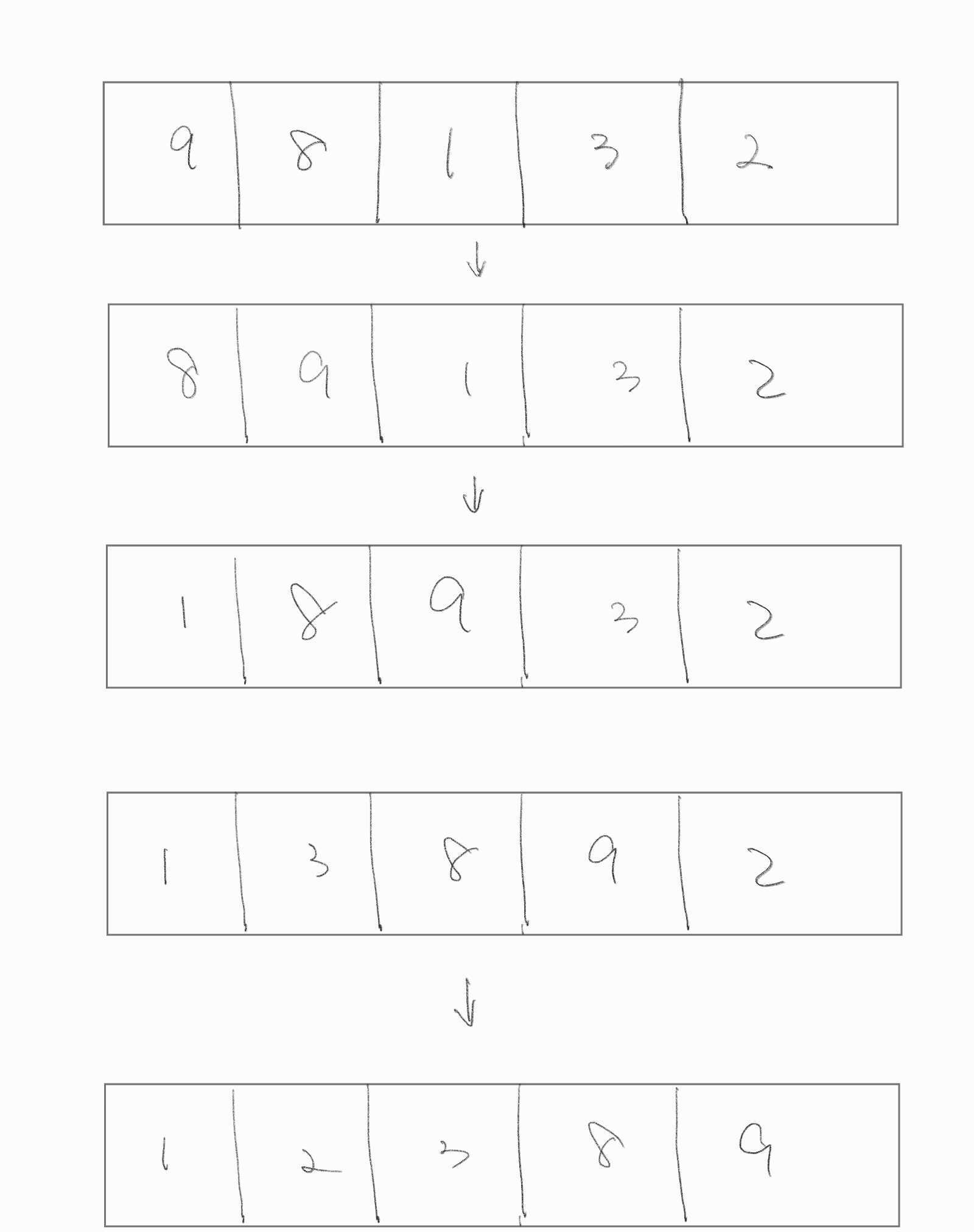
- 코드(KOTLIN)
import java.io.*
import java.util.*
fun main(args: Array<String>) {
val br = BufferedReader(InputStreamReader(System.`in`))
val n = br.readLine().toInt()
val st = StringTokenizer(br.readLine())
val numbers = IntArray(n) {
st.nextToken().toInt()
}
for (i in 1 until n) {
val key = numbers[i]
for (j in (i - 1) downTo 0) {
if (numbers[j] > key) {
// key 값을 앞으로 이동...
val temp = numbers[j]
numbers[j] = key
numbers[j + 1] = temp
}
}
}
for (num in numbers) {
print("$num ")
}
}728x90
'알고리즘' 카테고리의 다른 글
| [백준][KOTLIN] 2751 수 정렬하기 2 (0) | 2021.12.02 |
|---|---|
| [알고리즘][KOTLIN] 합병 정렬 - O(nlogn) (0) | 2021.12.01 |
| [백준][KOTLIN][1018]체스판 다시 칠하기 (0) | 2021.11.30 |
| [백준][KOTLIN][2231] 분해합 (0) | 2021.11.26 |
| [알고리즘][KOTLIN] 이진 탐색 (0) | 2021.11.22 |



